Du Noüy ring method
Method for measuring the surface tension of a liquid and the interfacial tension between two liquids. The force referred to the wetted length acting on a ring as a result of the tension of the withdrawn liquid lamella when moving the ring from one phase to another is measured in this method.
Background
A force maximum Fmax occurs when the lamella, which is produced when the ring moves through the phase boundary, is aligned vertically to the ring plane. This maximum correlates with the surface tension σ or interfacial tension according to the following equation:

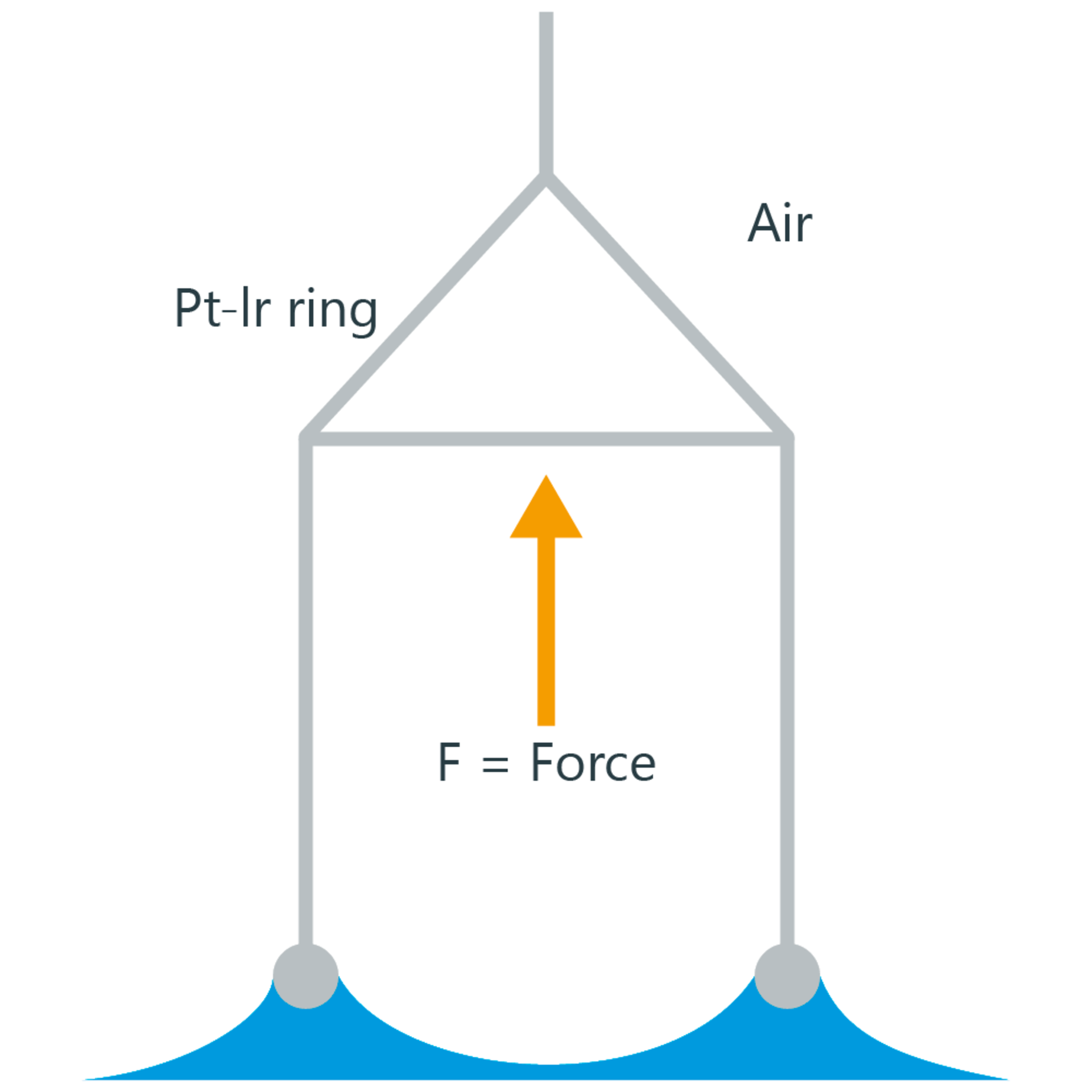
The wetted length L of the ring is the sum of the inner and outer circumference. Platinum-iridium is used as the material for the ring, as this alloy is optimally wettable due to its very high surface free energy and therefore generally forms a contact angle θ of 0° (cos θ = 1) with liquids. The material is also chemically inert and easy to clean.
The force maximum is determined with a modern tensiometer with the help of an electronic force sensor and can be obtained repeatedly without tearing the lamella. With a purely mechanical tensiometer, the maximum can only be determined by stretching the lamella until it detaches (ring tear-off method).
With the Du Noüy ring method, a correction must be made to the measurement, as the weight of the liquid of the lamella increases the measured force, and because the force maximum does not occur at the inside and outside of the lamella at the same time. Various correction methods, which are integrated into electronic KRÜSS tensiometers, exist based on tables which have been determined empirically by the authors Harkins and Jordan.
Because of the movement of the ring during the measurement, the ring method is only a quasi-static method which may not give the surface tension value at equilibrium for some samples. For such samples, the static Wilhelmy plate method is preferred for measuring the surface tension at equilibrium.


